解法別の記事第2弾となります!第1弾の“面積図”はこちらからご覧ください!今回の記事は面積図も少し出てきますので、そちらを理解してからの方がより効果的だと思います。
線分図は面積図と同じくらい、中学受験の根幹を担う解き方のひとつです。
想像つかない問題文や、計算が詰まった時、計算が合わなくなった時にこの線分図を使うことで対処できます。
それではまずは簡単な書き方からやっていきましょう!!
もうわかったから早く難しい問題が解きたいよ!という方は次のページから挑戦してみましょう!
- このページ:線分図の書き方、例題
- 2ページ目:和差算
- 3ページ目:流水算
- 4ページ目:数の性質
- 5ページ目:規則性
- 6ページ目:その他の単元、まとめ
となっております!!
⚠︎この記事では線分図に重きを置いて解説しているので、線分図に付随する解法などは省略して説明している場合があります。丁寧な解説をお求めの方にはリンクを挿入していますのでそちらでよりご覧ください!
何卒よろしくお願いします!
それでは行きましょう〜!!!!
線分図の書き方
線分図の書き方は面積図よりも極めて簡単です。面積図のようにたて×横ではなく、線の長さ=差となるので簡単にかけると思います。
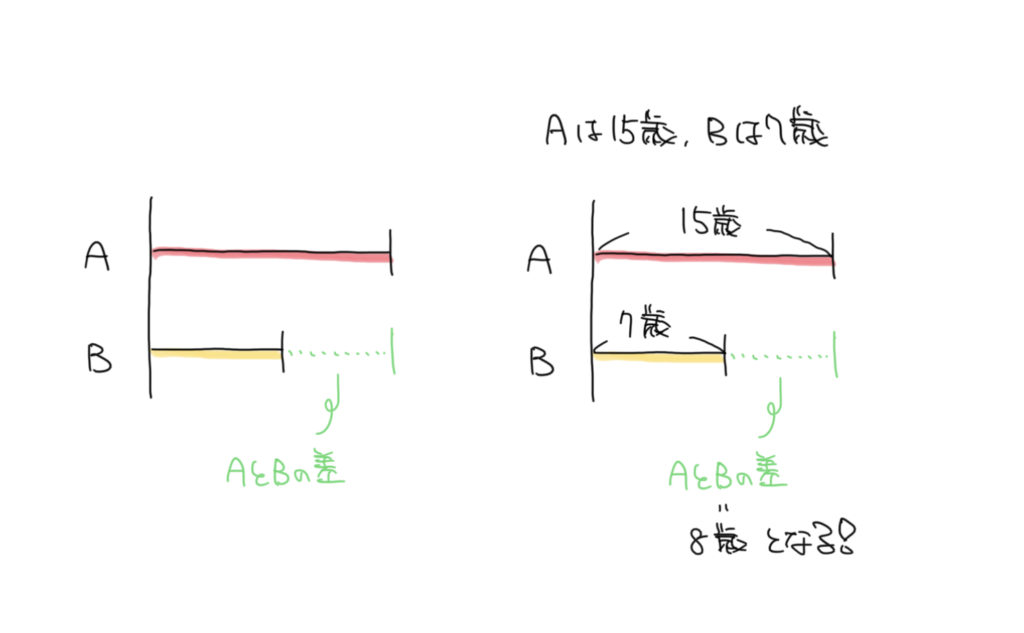
数の大きい方を長く、少ない方を短く書きます。緑の部分がAとBの差になります。
右の図はABの年齢を表しています。Aは15歳、Bは7歳何でAとBの差は15−7=8歳となります。
どうですか?面積図より簡単じゃないですか?
線分図には単位量あたりの数(○個/人や□km/時)がないので面積図より考えることが1個減ります。簡単な理由はそこにあります。
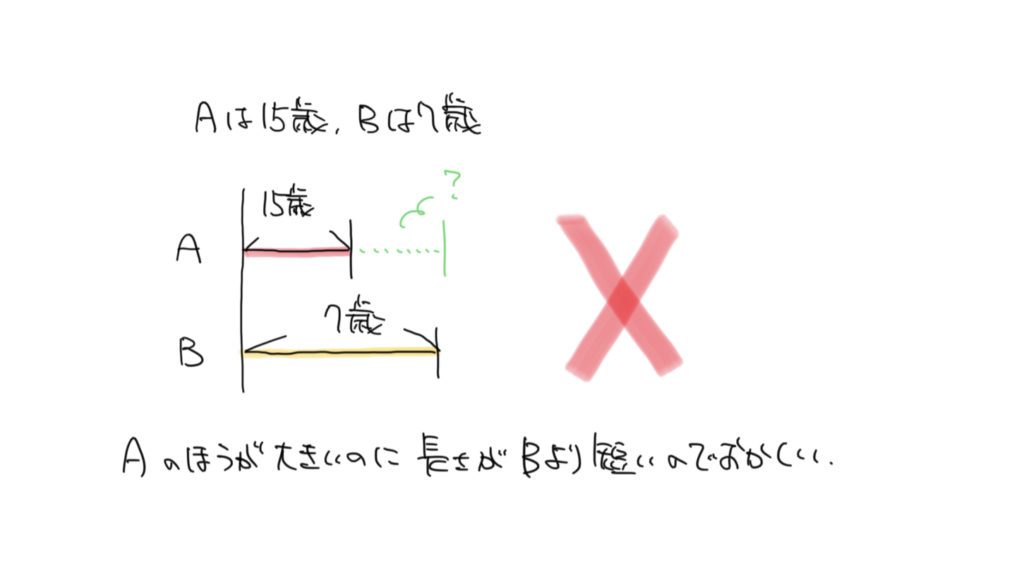
数が多いのに線の長さを短くすると差がおかしくなるので気をつけてください!!線分図の主な注意点はそこくらいです!
もちろん線分図ならではの難しさもあるので、しっかりそこも抑えていきましょう。
5つの例題にチャレンジ!!
[1]Aは16歳、Bは10歳です。2人の年齢の差は何歳ですか?
[2]Bの年齢は12歳です。Aの方が5歳年上の時、Aの年齢は何歳ですか?
[3]Aの年齢はBの2倍です。2人の年齢の差が7歳のとき、Aの年齢は何歳ですか?
[4]AとBとCの3人がいます。BとCの年齢差はAとBの年齢差の2倍です。Cが20歳、Bが16歳のとき、Aは何歳ですか?
[5]3本の鉛筆と消しゴム1つの代金は170円で、5本の消しゴムと消しゴム1つの値段は250円です。鉛筆1本の値段はいくらですか?
解答は下にあります!
[1]Aは16歳、Bは10歳です。2人の年齢の差は何歳ですか?
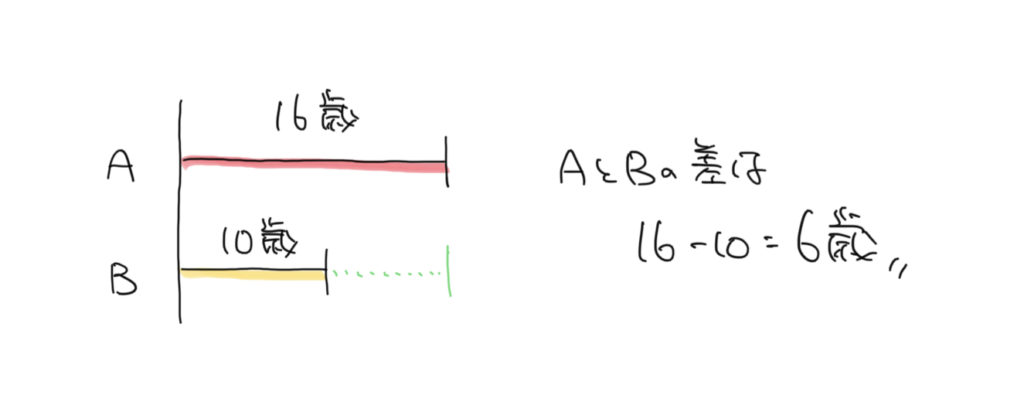
小学2年生とかでも解けちゃいそうな問題ですが、大事なのは線分図の書き方です!問題が解けても図が書けなかったら意味がありません。
しっかり描く練習をしましょう。単位や長さもチェックしてくださいね!
Aが16歳、Bが10歳なのでAの方が長くなります。Bの情報も書き込めば、差が6歳と求められます。
[2]Bの年齢は12歳です。Aの方が5歳年上の時、Aの年齢は何歳ですか?
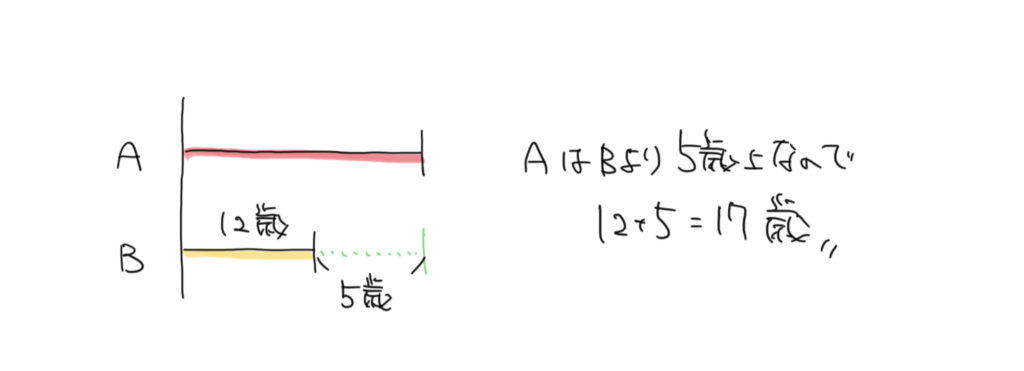
Aの年齢がわかっておらず、Bの年齢と差がわかっています。線分図に書くと上のような感じです。
よってAの年齢を17歳と求めることができます。
さて、ここからすこ〜し難易度が上がります!
[3]Aの年齢はBの2倍です。2人の年齢の差が7歳のとき、Aの年齢は何歳ですか?
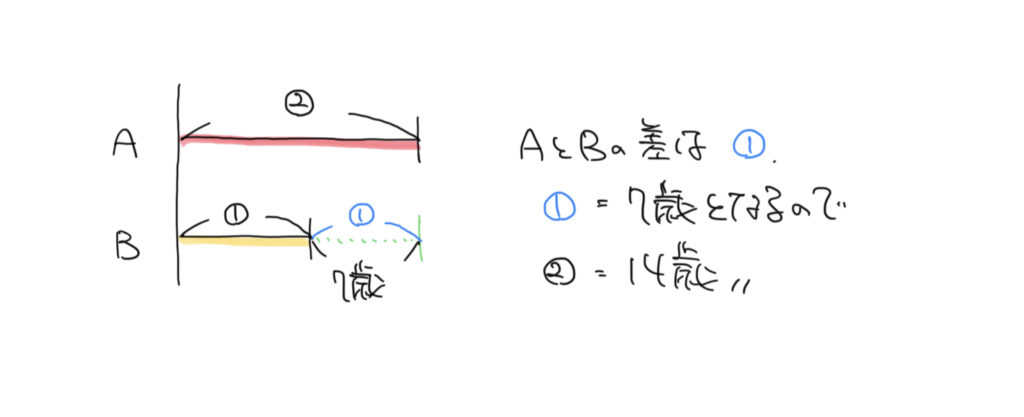
仮定の考えが出てきます。仮定とは計算をときやすくするための思考法のひとつです。AがBの2倍の年齢ということがわかっているので、
Bの年齢を①とすると、Aの年齢が②と求めることができます。
2人の年齢の差は②−①=①歳なので、①=7となります。
よってAの年齢である②歳=14歳です。
[4]AとBとCの3人がいます。BとCの年齢差はAとBの年齢差の2倍です。Cが20歳、Bが16歳のとき、Aは何歳ですか?
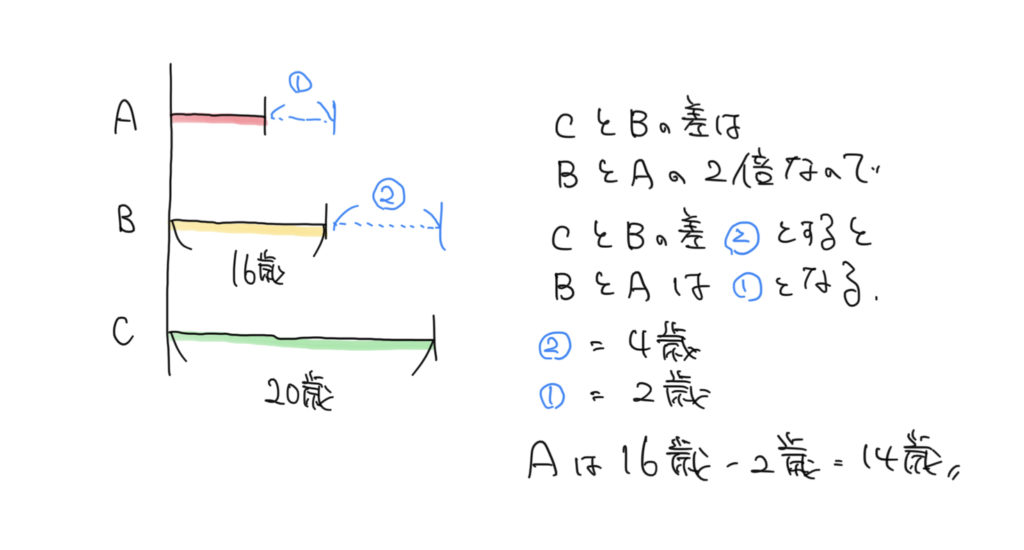
3人出てきますが、同じく仮定を使って考えましょう。
繰り返しですが、この問題たちは解けることよりも図を正確に描けることの方が重要です。
必ず図を徹底して書くようにしましょう。
AとBの差を①とすると、CとBの差は②となります。これを図に入れて考えると、②=20歳−16歳=4歳であることがわかります。
よって①=2歳。Aの年齢は16歳−①で表されるので、16歳−2歳=14歳となります。
[5]3本の鉛筆と消しゴム1つの代金は170円で、5本の消しゴムと消しゴム1つの値段は250円です。鉛筆1本の値段はいくらですか?
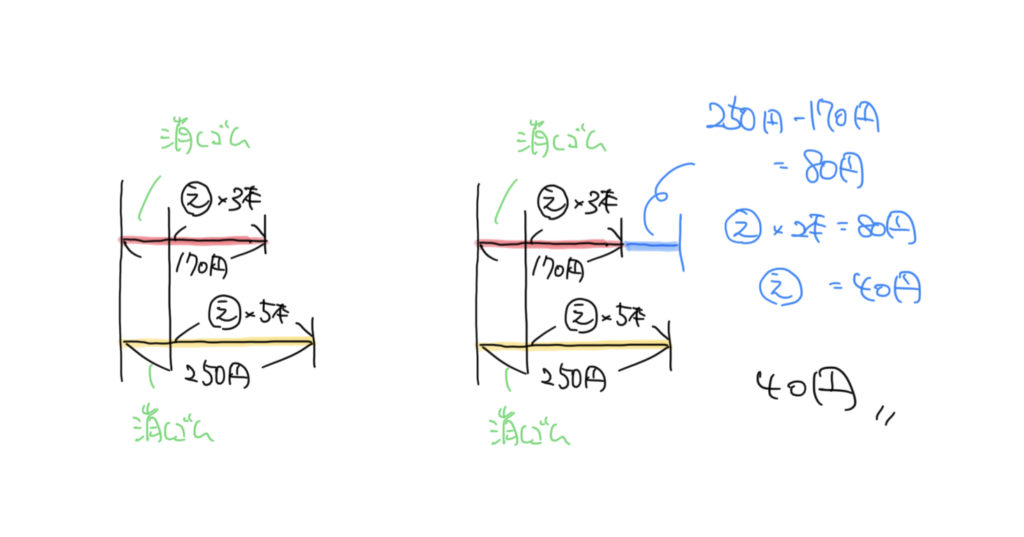
代金の問題もこのように線分図を書いて求めることができました。消しゴムに値段が同じというところがポイントでした。
なので金額の差=鉛筆2本分の代金となり、求めることができます。
これについては和差算でも詳しくやるので、そちらも確認してみてください。
さて、ここまでが線分図の超基礎でした。
ここからは線分図を使う単元、和差算、流水算、数の性質などの問題に取り掛かりましょう!!
- このページ:線分図の書き方、例題
- 2ページ目:和差算
- 3ページ目:流水算
- 4ページ目:数の性質
- 5ページ目:規則性
- 6ページ目:その他の単元、まとめ










コメント